The non-equilibrium characteristics of active matter

Yuting Li (Irene)

Soft matter group, DAMTP

What is active matter?

  1. Processes that locally inject energy into the environment
  2. Non-equilibrium; no time reversal symmetry; no Boltzmann distribution etc

Why should I care?

Myosin walking on actin (Prost et al, Nat phys, 2015) Microtubule bundles and kinesin
(Giomi PRX 2015)

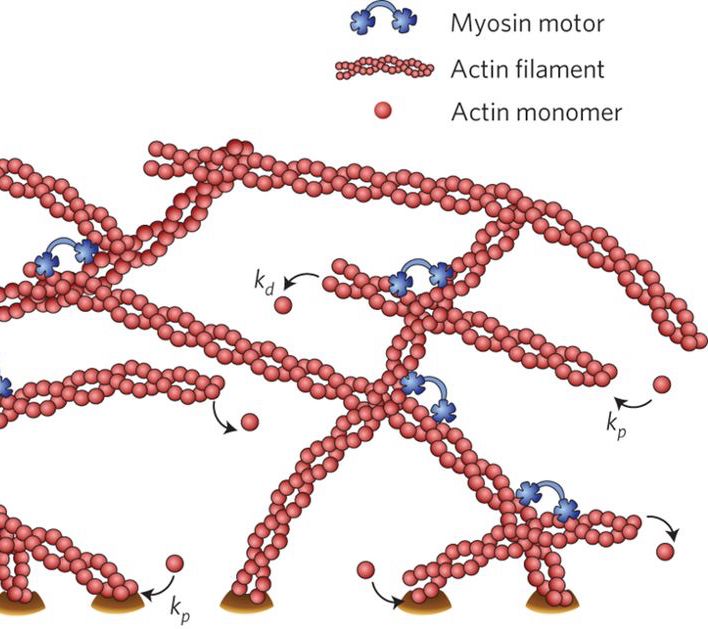
Why should I care?

Bacterial ratchet motors
(Di Leonardo et all PNAS 2010) 		Self-propelling discs
(Briand, Schindler, Dauchot PRL 2018)

Why should I care?

Self-propelled hard colloids without alignment

(Redner PRL 2013)

Minimal model for self-propelled bacteria with quorum sensing

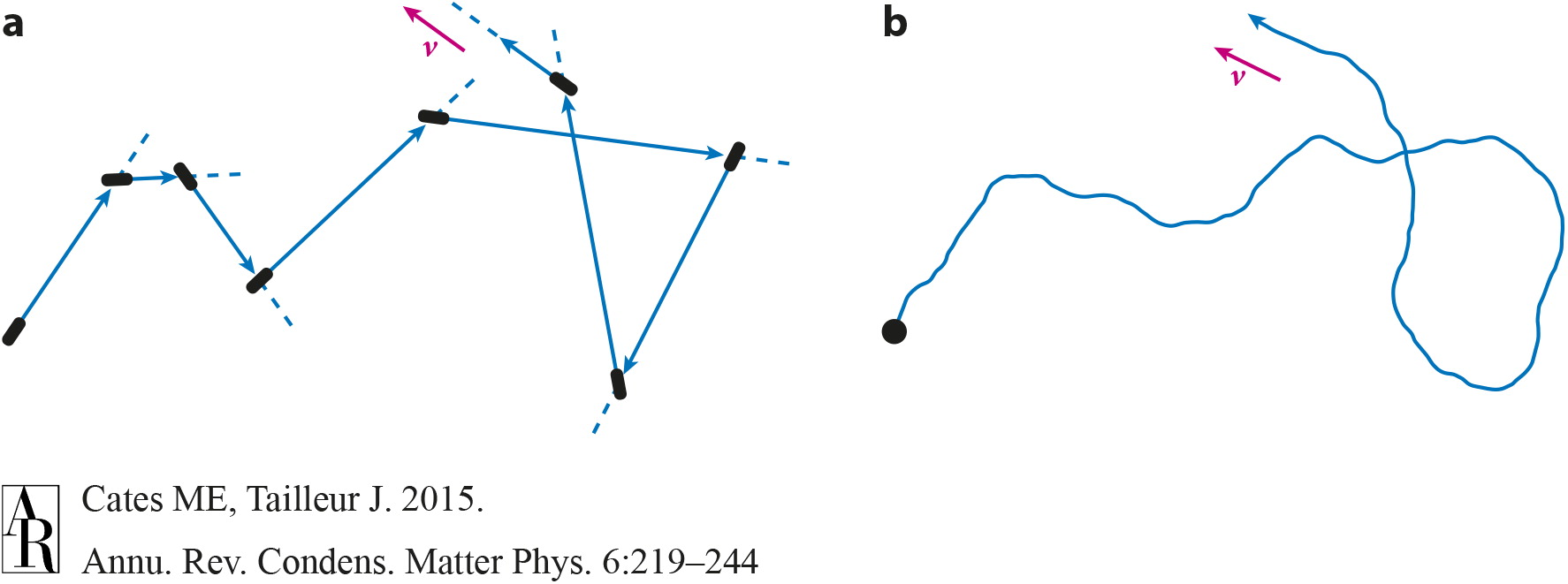
Two approches

  1. Explicitly coarse-grain from microscopic rules
  2. Make an intelligent guess
The intelligent guess approach

Expand $\rho(x, t) = \rho_\mathrm{ref} ( 1 + \phi(x, t)) $

Require rotational symmetry, translational symmetry, conservation of $\phi$

\begin{equation} \begin{split} \partial_t \phi & = - \nabla \cdot \mathbf{J} \\ \mathbf{J} & = - \nabla \mu + \fbox{$\zeta (\nabla^2 \phi) \nabla \phi$} + \sqrt{2D} \mathbf{\Lambda} \\ \mu & = \alpha \phi + \beta \phi^3 - \kappa \nabla^2 \phi + \fbox{$\lambda (\nabla \phi )^2$} \end{split} \end{equation}
What about time reversal symmetry?

  • Consider the trajectory $\phi(t)_{t \in [0, T]}$

    \begin{equation} \mathbb{P}[\phi(t)_{t \in [0, T]}] = \mathbb{P} [ \phi(t)_{t \in [0, T]} | \phi(0)] P(\phi(0)) \end{equation}

  • Consider the reversed trajectory $\phi^\mathrm{R}(t) \equiv \phi(T-t)$

    \begin{equation} \mathbb{P}[\phi^R(t)_{t \in [0, T]}] = \mathbb{P} [ \phi^R(t)_{t \in [0, T]} | \phi(T)] P(\phi(T)) \end{equation}

  • $\mathbb{P}[\phi^R(t)_{t \in [0, T]}] = \mathbb{P}[\phi(t)_{t \in [0, T]}]$ iff

    \begin{equation} R[\phi(t)] \equiv \frac{\mathbb{P} [ \phi(t)_{t \in [0, T]} | \phi(0)]}{\mathbb{P} [ \phi^R(t)_{t \in [0, T]} | \phi(T)]} = \frac{P(\phi(T))}{P(\phi(0))} \end{equation}

In our model $\partial_t \phi = - \nabla \cdot \mathbf{J}_\mathrm{d} - \sqrt{2D} \nabla \cdot \Lambda$

Probability of a trajectory $\phi(t)_{t \in [0, T]}$,

\begin{equation} \mathbb{P} [ \phi(t)_{[0, T]} | \phi(0)] \propto \exp \left [ - \int \mathrm{d}x \mathrm{d}t \frac{1}{4D} \left | \nabla^{-1} (\partial_t \phi + \nabla \cdot \mathbf{J}_\mathrm{d})\right |^2 \right ] \end{equation}

Time reversal $\partial_t \phi^R = - \partial_t \phi$,

\begin{equation} R[\phi(t)] = \exp \left [ - \int \mathrm{d}x\mathrm{d}t \frac{1}{D} \partial_t \phi \left ( \mu + \zeta (\dots) \right )\right ] \end{equation}

In general, $R(\phi)$ not a function of the endpoints, but if $\zeta = \lambda = 0$,

\begin{equation} \mu(x, t)= \frac{\delta F[\phi(t)]}{\delta \phi(x, t)} \rightarrow R[\phi] = \exp \left [ - \frac{1}{D} (F[\phi(T)] - F[\phi(0)]) \right ] \end{equation}
Consequences of the TRS-breaking terms
(Tjhung, Nardini, Cates, PRX 2018)
What if we break mass conservation?
  • Population dynamics of bacteria
  • Birth via cell splitting + competition for resources $\partial_t \rho = - u \rho ( \rho - \rho_\mathrm{t} )$
  • In terms of our expansion parameter $\phi$, $\partial_t \phi = \nabla^2 \mu_\mathrm{eq}- u (\phi + \rho_\mathrm{ref})(\phi - \phi_\mathrm{t})$
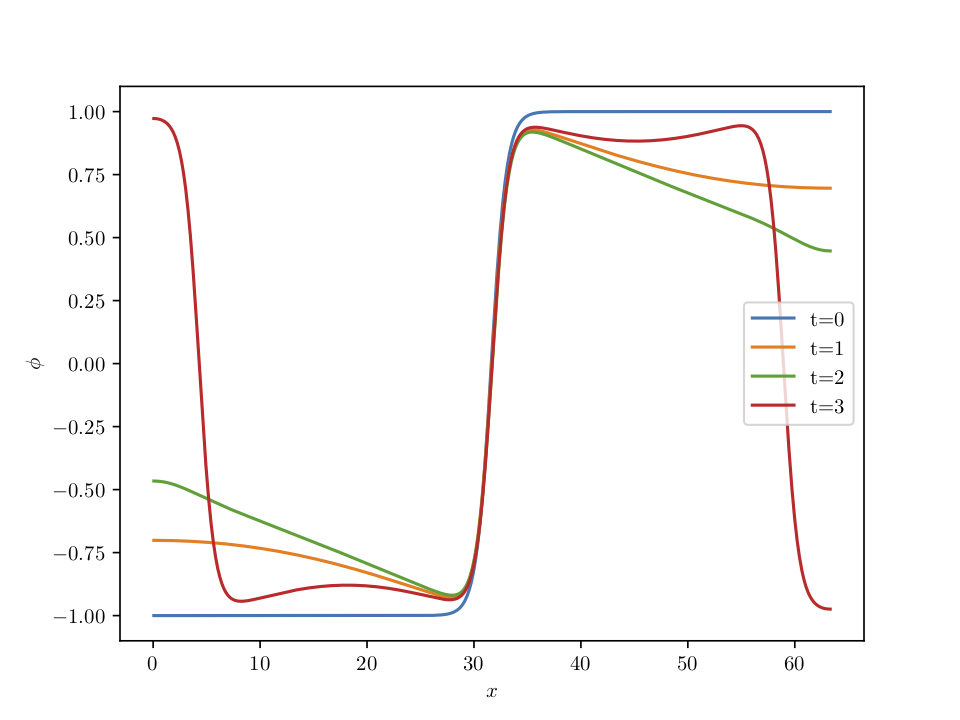
The limit cycle phase
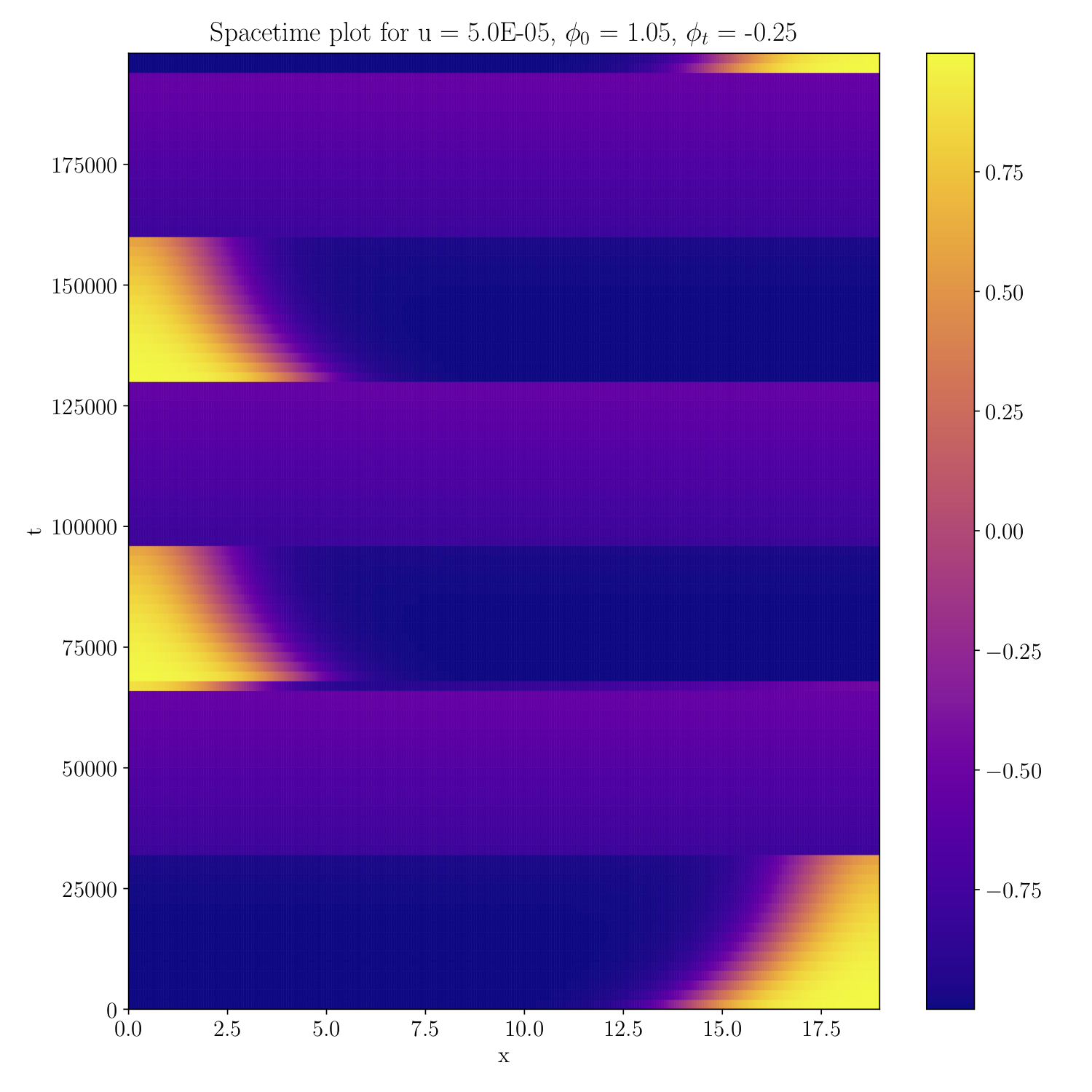
The arrested steady state phase

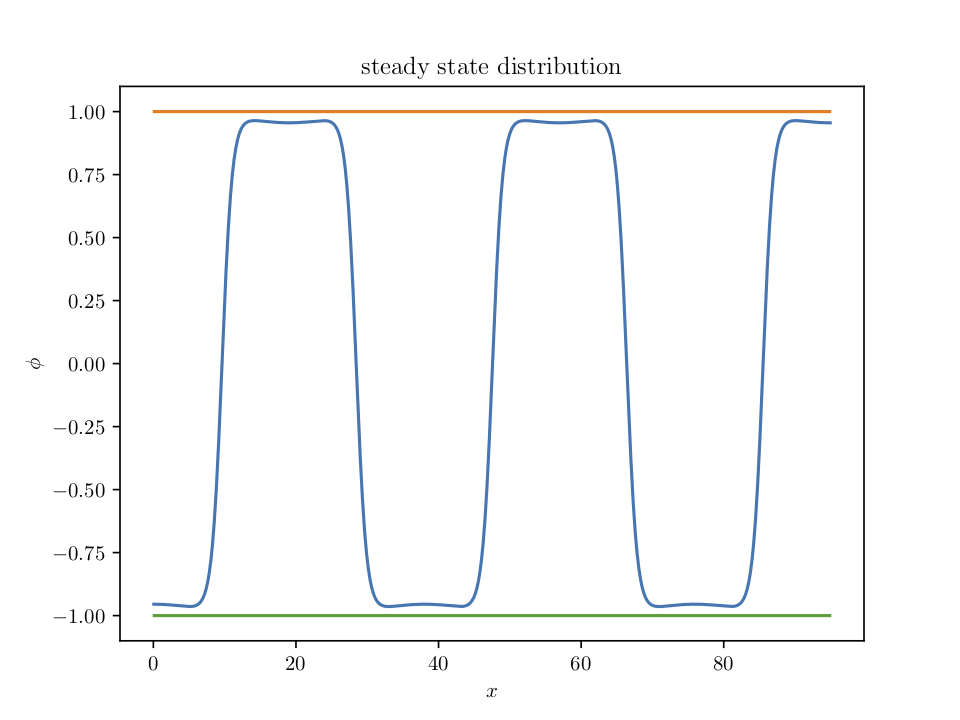
Thank you!

This presentation: https://irene-li.github.io/tms_talk